GPU computing with Chapel

Table of contents

October 1st, 2024^st
10:00am–11:00am Pacific Time

Chapel was designed as a parallel-first programming language targeting any hardware that supports parallel execution: multicore processors, multiple nodes in an HPC cluster, and now also GPUs on HPC systems. This is very different from the traditional approach to parallel programming in which you would use a dedicated tool for each level of hardware parallelism, e.g. MPI, or OpenMP, or CUDA, etc.

Towards of the end of this webinar I will show a compact Chapel code that uses multiple nodes on a cluster, multiple GPUs on each node, and automatically utilizes all available (in our Slum job) CPU cores on each node, while copying the data as needed between all these hardware layers. But let’s start with the basics!

Running GPU Chapel on the Alliance systems

In general, you need to configure and compile Chapel for your specific GPU type and your specific cluster interconnect. For NVIDIA and AMD GPUs (the only ones currently supported), you must use LLVM as the backend compiler. With NVIDIA GPUs, you must build LLVM to use LLVM’s NVPTX backend to support GPU programming, so usually you cannot use the system-provided LLVM module – instead you should set CHPL_LLVM=bundled during Chapel compilation.

As of this writing, on the Alliance systems, you can use GPUs from Chapel on the following systems:

native multi-locale on Cedar
on an Arbutus VM in a project with access to vGPUs
via a single-locale GPU Chapel container on any Alliance system (clusters, cloud) with NVIDIA GPUs

Efforts are underway to expand native GPU Chapel support to more systems in the Alliance.

Running GPU Chapel on your computer

If you have an NVIDIA GPU on your computer and run Linux, and have all the right GPU drivers and CUDA installed, it should be fairly straightforward to compile Chapel with GPU support. Here is what worked for me in AlmaLinux 9.4. Please let me know if these steps do not work for you.

In Windows, Chapel with GPU support works under the Windows Subsystem for Linux (WSL) as explained in this post. You could also run Chapel inside a Docker container, although you need to find a GPU-enabled Docker image.

Useful built-in variables

From inside your Chapel code, you can access the following predefined variables:

Locales is the list of locales (nodes) that your code can run on (invoked in code execution)
numLocales is the number of these locales
here is the current locale (node), and by extension current CPU
here.name is its name
here.maxTaskPar is the number of CPU cores on this locale
here.gpus is the list of available GPUs on this locale (sometimes called “sublocales”)
here.gpus.size is the number of available GPUs on this locale
here.gpus[0] is the first GPU on this locale

Let’s try some of these out on Cedar:

source /home/razoumov/startMultiLocaleGPU.sh
cd ~/scratch
salloc --time=2:0:0 --nodes=1 --cpus-per-task=1 --mem-per-cpu=3600 --gpus-per-node=v100l:1 \
	   --account=cc-debug --reservation=asasfu_756
git clone ~/chapelBare/ $SLURM_TMPDIR
cd $SLURM_TMPDIR/gpu

writeln("Locales: ", Locales);
writeln("on ", here.name, " I see ", here.gpus.size, " GPUs");
writeln("and their names are: ", here.gpus);

chpl --fast probeGPU.chpl
./probeGPU -nl 1

Locales: LOCALE0
on cdr2514.int.cedar.computecanada.ca I see 1 GPUs
and their names are: LOCALE0-GPU0

There is one GPU, and it is available to us as the first (and only) element of the array here.gpus.

Our first GPU code

To benefit from GPU acceleration, you want to run a computation that can be broken into many independent identical pieces. An obvious example is a for loop in which each loop iteration does not depend on other iterations. Let’s run such an example on the GPU:

config const n = 10;
on here.gpus[0] {
  var A: [1..n] int;     // kernel launch to initialize an array
  foreach i in 1..n do   // thread parallelism on a CPU or a GPU => kernel launch
    A[i] = i**2;
  writeln("A = ", A);    // copy A to host
}

A = 1 4 9 16 25 36 49 64 81 100

the array A is stored on the GPU
order-independent loops will be executed in parallel on the GPU
if instead of parallel foreach we use serial for, the loop will run on the CPU
in our case the array A is both stored and computed on the GPU in parallel
currently, to be computed on a GPU, an array must be stored on that GPU
in general, when you run a code block on the device, parallel lines inside will launch kernels

Alternative syntax

We can modify this code so that it runs on a GPU if present; otherwise, it will run on the CPU:

var operateOn =
  if here.gpus.size > 0 then here.gpus[0]   // use the first GPU
  else here;                                // use the CPU
writeln("operateOn: ", operateOn);
config const n = 10;
on operateOn {
  var A: [1..n] int;
  foreach i in 1..n do
    A[i] = i**2;
  writeln("A = ", A);
}

Demo

Let try running this both with and without a GPU.

You can also force a GPU check by hand:

if here.gpus.size == 0 {
  writeln("need a GPU ...");
  exit(1);
}

GPU diagnostics

Wrap our code into the following lines:

use GpuDiagnostics;
startGpuDiagnostics();
...
stopGpuDiagnostics();
writeln(getGpuDiagnostics());

operateOn: LOCALE0-GPU0
A = 1 4 9 16 25 36 49 64 81 100
(kernel_launch = 2, host_to_device = 0, device_to_host = 10, device_to_device = 0)

Let’s break down the events:

we have two kernel launches

  var A: [1..n] int;     // kernel launch to initialize an array
  foreach i in 1..n do   // kernel launch to run a loop in parallel
    A[i] = i**2;

we copy 10 array elements device-to-host to print them

  writeln("A = ", A);

no other data transfer

Let’s take a look at the example from https://chapel-lang.org/blog/posts/intro-to-gpus. They define a function:

use GpuDiagnostics;
proc numKernelLaunches() {
  stopGpuDiagnostics();
  var result = getGpuDiagnostics().kernel_launch;
  resetGpuDiagnostics();
  startGpuDiagnostics();
  return result;
}

which can then be applied to these 3 examples (all in one on here.gpus[0] block):

  // --- example 1
startGpuDiagnostics();
on here.gpus[0] {
  var E = 2 * [1,2,3,4,5]; // one kernel launch to initialize the array
  writeln(E);
  assert(numKernelLaunches() == 1);

  use Math;
  const n = 10;
  var A = [i in 0..#n] sin(2 * pi * i / n); // one kernel launch
  writeln(A);
  assert(numKernelLaunches() == 1);

  var rows, cols = 1..5;
  var Square: [rows, cols] int;         // one kernel launch
  foreach (r, c) in Square.indices do   // one kernel launch
    Square[r, c] = r * 10 + c;
  writeln(Square);
  assert(numKernelLaunches() == 2);
}

Verifying if a loop can run on a GPU

The loop attribute @assertOnGpu (applied to a loop) does two things:

at compilation, will fail to compile a code that cannot run on a GPU and will tell you why
at runtime, will halt execution if called from outside a GPU

Consider the following serial code:

config const n = 10;
on here.gpus[0] {
  var A: [1..n] int;
  for i in 1..n do
    A[i] = i**2;
  writeln("A = ", A);
}

A = 1 4 9 16 25 36 49 64 81 100

This code compiles fine (chpl --fast test.chpl), and it appears to run fine, printing the array. But it does not run on the GPU! Let’s mark the for loop with @assertOnGpu and try to compile it again. Now we get:

error: loop marked with @assertOnGpu, but 'for' loops don't support GPU execution

Serial for loops cannot run on a GPU! Without @assertOnGpu the code compiled for and ran on the CPU. To port this code to the GPU, replace for with either foreach or forall (both are parallel loops), and it should compile with @assertOnGpu.

Alternatively, you can count kernel launches – it’ll be zero for the for loop.

More on @assertOnGpu and other attributes at https://chapel-lang.org/docs/main/modules/standard/GPU.html.

In Chapel 2.2 there is a new additional attribute @gpu.assertEligible that asserts that a statement is suitable for GPU execution (same as @assertOnGpu), without requiring it to be executed on a GPU.

Timing on the CPU

Let’s pack our computation into a function, so that we can call it from both a CPU and a GPU. For timing, we can use a stopwatch from the Time module:

use Time;

config const n = 10;
var watch: stopwatch;

proc squares(device) {
  on device {
    var A: [1..n] int;
    foreach i in 1..n do
      A[i] = i**2;
    writeln("A = ", A[n-2..n]); // last 3 elements
  }
}

writeln("--- on CPU:"); watch.start();
squares(here);
watch.stop(); writeln('It took ', watch.elapsed(), ' seconds');

watch.clear();

writeln("--- on GPU:"); watch.start();
squares(here.gpus[0]);
watch.stop(); writeln('It took ', watch.elapsed(), ' seconds');

$ chpl --fast test.chpl
$ ./test -nl 1 --n=100_000_000
--- on CPU:
A = 9999999600000004 9999999800000001 10000000000000000
It took 7.94598 seconds
--- on GPU:
A = 9999999600000004 9999999800000001 10000000000000000
It took 0.003673 seconds

You can also call start and stop functions from inside the on device block – they will still run on the CPU. We will see an example of this later in this webinar.

Timing on the GPU

Obtaining timing from within a running CUDA kernel is tricky as you are running potentially thousands of simultaneous threads, so you definitely cannot measure the wallclock time. However, you can measure GPU clock cycles spent on a partucular part of the kernel function. The GPU module provides a function gpuClock() that returns the clock cycle counter (per multiprocessor), and it needs to be called to time code blocks within a GPU-enabled loop.

Here is an example (modelled after measureGpuCycles.chpl) to demonstrate its use. This is not the most efficient code, as on the GPU we are parallelizing the loop with n=10 iterations, and then inside each iteration we run a serial loop to keep the (few non-idle) GPU cores busy, but it gives you an idea.

use GPU;

config const n = 10;

on here.gpus[0] {
  var A: [1..n] int;
  var clockDiff: [1..n] uint;
  @assertOnGpu foreach i in 1..n {
    var start, stop: uint;
    A[i] = i**2;
    start = gpuClock();
    for j in 0..<1000 do
      A[i] += i*j;
    stop = gpuClock();
    clockDiff[i] = stop - start;
  }
  writeln("Cycle count = ", clockDiff);
  writeln("Time = ", (clockDiff[1]: real) / (gpuClocksPerSec(0): real), " seconds");
  writeln("A = ", A);
}

Cycle count = 227132 227132 227132 227132 227132 227132 227132 227132 227132 227132
Time = 0.148452 seconds
A = 49501 49604 49709 49816 49925 50036 50149 50264 50381 50500

Prime factorization of each element of a large array

Now let’s compute a more interesting problem where we do some significant processing of each element, but independently of other elements – this will port nicely to a GPU.

Prime factorization of an integer number is finding all its prime factors. For example, the prime factors of 60 are 2, 2, 3, and 5. Let’s write a function that takes an integer number and returns the sum of all its prime factors. For example, for 60 it will return 2+2+3+5 = 12, for 91 it will return 7+13 = 20, for 101 it will return 101, and so on.

proc primeFactorizationSum(n: int) {
  var num = n, output = 0, count = 0;
  while num % 2 == 0 {
    num /= 2;
    count += 1;
  }
  for j in 1..count do output += 2;
  for i in 3..(sqrt(n:real)):int by 2 {
    count = 0;
    while num % i == 0 {
      num /= i;
      count += 1;
    }
    for j in 1..count do output += i;
  }
  if num > 2 then output += num;
  return output;
}

Since 1 has no prime factors, we will start computing from 2, and then will apply this function to all integers in the range 2..n, where n is a larger number. We will do all computations separately from scratch for each number, i.e. we will not cache our results (caching could potentially speed up our calculations but the point here is to focus on brute-force computing).

With the procedure primeFactorizationSum defined, here is the CPU version:

config const n = 10;
var A: [2..n] int;
for i in 2..n do
  A[i] = primeFactorizationSum(i);

var lastFewDigits =
  if n > 5 then n-4..n  // last 5 digits
  else 2..n;            // or fewer

writeln("A = ", A[lastFewDigits]);

Here is the GPU version:

config const n = 10;
on here.gpus[0] {
  var A: [2..n] int;
  @assertOnGpu foreach i in 2..n do
    A[i] = primeFactorizationSum(i);
  var lastFewDigits =
    if n > 5 then n-4..n  // last 5 digits
    else 2..n;            // or fewer
  writeln("A = ", A[lastFewDigits]);
}

chpl --fast primesSerial.chpl
./primesSerial -nl 1 --n=10_000_000
chpl --fast primesGPU.chpl
./primesGPU -nl 1 --n=10_000_000

In both cases we should see the same output:

A = 4561 1428578 5000001 4894 49

Let’s add timing to both codes:

use Time;
var watch: stopwatch;
...
watch.start();
...
watch.stop(); writeln('It took ', watch.elapsed(), ' seconds');

Note that this problem does not scale linearly with n, as with larger numbers you will get more primes. Here are my timings on Cedar’s V100 GPU:

n	CPU time in sec	GPU time in sec
1_000_000	3.04051	0.001649
10_000_000	92.8213	0.042215
100_000_000	2857.04	1.13168

Finer control

There are various settings that you can fine-tune via attributes for maximum performance, e.g. you can change the number of threads per block (default 512, should be a multiple of 32) when launching kernels:

 @gpu.blockSize(64) foreach i in 1..128 { ...}

You can also change the default when compiling Chapel via CHPL_GPU_BLOCK_SIZE variable, or when compiling Chapel codes by passing the flag --gpu-block-size=<block_size> to Chapel compiler

Another setting to play with is the number of iterations per thread:

@gpu.itersPerThread(4) foreach i in 1..128 { ... }

This setting is probably specific to your computational problem. For these and other per-kernel attributes, please see this page.

Multiple locales and multiple GPUs

If we have access to multiple locales and then multiple GPUs on each of those locales, we would utilize all this processing power through two nested loops, first cycling through all locales and then through all available GPUs on each locale:

coforall loc in Locales do
  on loc {
    writeln("on ", loc.name, " I see ", loc.gpus.size, " GPUs");
    coforall gpu in loc.gpus {
	  on gpu {
		... do some work in parallel ...
	  }
    }
  }

Here we assume that we are running inside a multi-node job on the cluster, e.g.

salloc --time=1:0:0 --nodes=3 --mem-per-cpu=3600 --gpus-per-node=2 --account=...
chpl --fast test.chpl
./test -nl 3

How would we use this approach in practice? Let’s consider our primes factorization problem. Suppose we want to collect the results on one node (LOCALE0), maybe for printing or for some additional processing. We need to break our array A into pieces, each computed on a separate GPU from the total pool of 6 GPUs available to us inside this job. Here is our approach, following the ideas outlined in https://chapel-lang.org/blog/posts/gpu-data-movement :

import RangeChunk.chunks;

proc primeFactorizationSum(n: int) {
  ...
}

config const n = 1000;
var A_on_host: [2..n] int;   // suppose we want to collect the results on one node (LOCALE0)

// let's assume that numLocales = 3

coforall (loc, locChunk) in zip(Locales, chunks(2..n, numLocales)) {
  /* loc=LOCALE0, locChunk=2..334 */
  /* loc=LOCALE1, locChunk=335..667 */
  /* loc=LOCALE2, locChunk=668..1000 */
  on loc {
    writeln("loc = ", loc, "   chunk = ", locChunk);
	const numGpus = here.gpus.size;
	coforall (gpu, gpuChunk) in zip(here.gpus, chunks(locChunk, numGpus)) {
	  /* on LOCALE0 will see gpu=LOCALE0-GPU0, gpuChunk=2..168 */
	  /*                     gpu=LOCALE0-GPU1, gpuChunk=169..334 */
	  on gpu {
		writeln("loc = ", loc, "   gpu = ", gpu, "   chunk = ", gpuChunk);
		var A_on_device: [gpuChunk] int;
		foreach i in gpuChunk do
		  A_on_device[i] = primeFactorizationSum(i);
		A_on_host[gpuChunk] = A_on_device; // copy the chunk from the GPU via the host to LOCALE0
	  }
	}
  }
}

var lastFewDigits = if n > 5 then n-4..n else 2..n;   // last 5 or fewer digits
writeln("last few A elements: ", A_on_host[lastFewDigits]);

The array A_on_host resides entirely in host’s memory on one node. With a sufficiently large problem, you can distribute A_on_host across multiple nodes using block distribution:

use BlockDist; // use standard block distribution module to partition the domain into blocks
config const n = 1000;
const distributedMesh: domain(1) dmapped new blockDist(boundingBox={2..n}) = {2..n};
var A_on_host: [distributedMesh] int;

This way, when copying from device to host, you will copy only to the locally stored part of A_on_host.

Demo

Let’s run this code with 2 GPUs on one Cedar node:

source /home/razoumov/startMultiLocaleGPU.sh
cd ~/scratch
salloc --time=2:0:0 --nodes=1 --cpus-per-task=1 --mem-per-cpu=3600 --gpus-per-node=v100l:2 \
	   --account=cc-debug --reservation=asasfu_756
git clone ~/chapelBare/ $SLURM_TMPDIR
cd $SLURM_TMPDIR/primeFactorization
chpl --fast primesGPU-distributed.chpl
./primesGPU-distributed -nl 1

loc = LOCALE0   chunk = 2..1000
loc = LOCALE0   gpu = LOCALE0-GPU0   chunk = 2..501
loc = LOCALE0   gpu = LOCALE0-GPU1   chunk = 502..1000
last few A elements: 90 997 501 46 21

Demo

Now run the same code on a computer without GPUs.

Use GPU features without a GPU and/or vendor SDK

You can recompile Chapel in so-called ‘CPU-as-device’ mode by setting export CHPL_GPU=cpu and use GPU code on a CPU, even if your computer does not have a GPU and/or vendor SDK installed. This is very useful for debugging a Chapel GPU code on a computer without a dedicated GPU. You can find more details on this mode here.

You can also use some of the Chapel’s diagnostic features in this mode, e.g. the @assertOnGpu attribute will fail at compile time for ineligible loops. You will also get the correct kernel launch count, but data movement between the device and the host will not be captured (as there is no data moved).

As far as I can tell, Homebrew’s Chapel in MacOS was compiled in this mode.

I also compiled a single-locale ‘CPU-as-device’ Chapel version on Cedar:

source /home/razoumov/startSingleLocaleCPUasDevice.sh
git clone ~/chapelBare 111
cd 111/gpu
chpl --fast probeGPU.chpl
./probeGPU

The GPU kernels are launched on the CPU.

In my experience, some parallel operations (e.g. reductions) are not available in this mode.

Porting the Julia set problem to a GPU

In the Julia set problem we need to compute a set of points on the complex plane that remain bound under infinite recursive transformation $f(z)$. We will use the traditional form $f(z)=z^2+c$, where $c$ is a complex constant. Here is our algorithm:

pick a point $z_0\in\mathbb{C}$
compute iterations $z_{i+1}=z_i^2+c$ until $|z_i|>4$ (arbitrary fixed radius; here $c$ is a complex constant)
store the iteration number $\xi(z_0)$ at which $z_i$ reaches the circle $|z|=4$
limit max iterations at 255
4.1 if $\xi(z_0)=255$, then $z_0$ is a stable point
4.2 the quicker a point diverges, the lower its $\xi(z_0)$ is
plot $\xi(z_0)$ for all $z_0$ in a rectangular region $-1<=\mathfrak{Re}(z_0)<=1$, $-1<=\mathfrak{Im}(z_0)<=1$

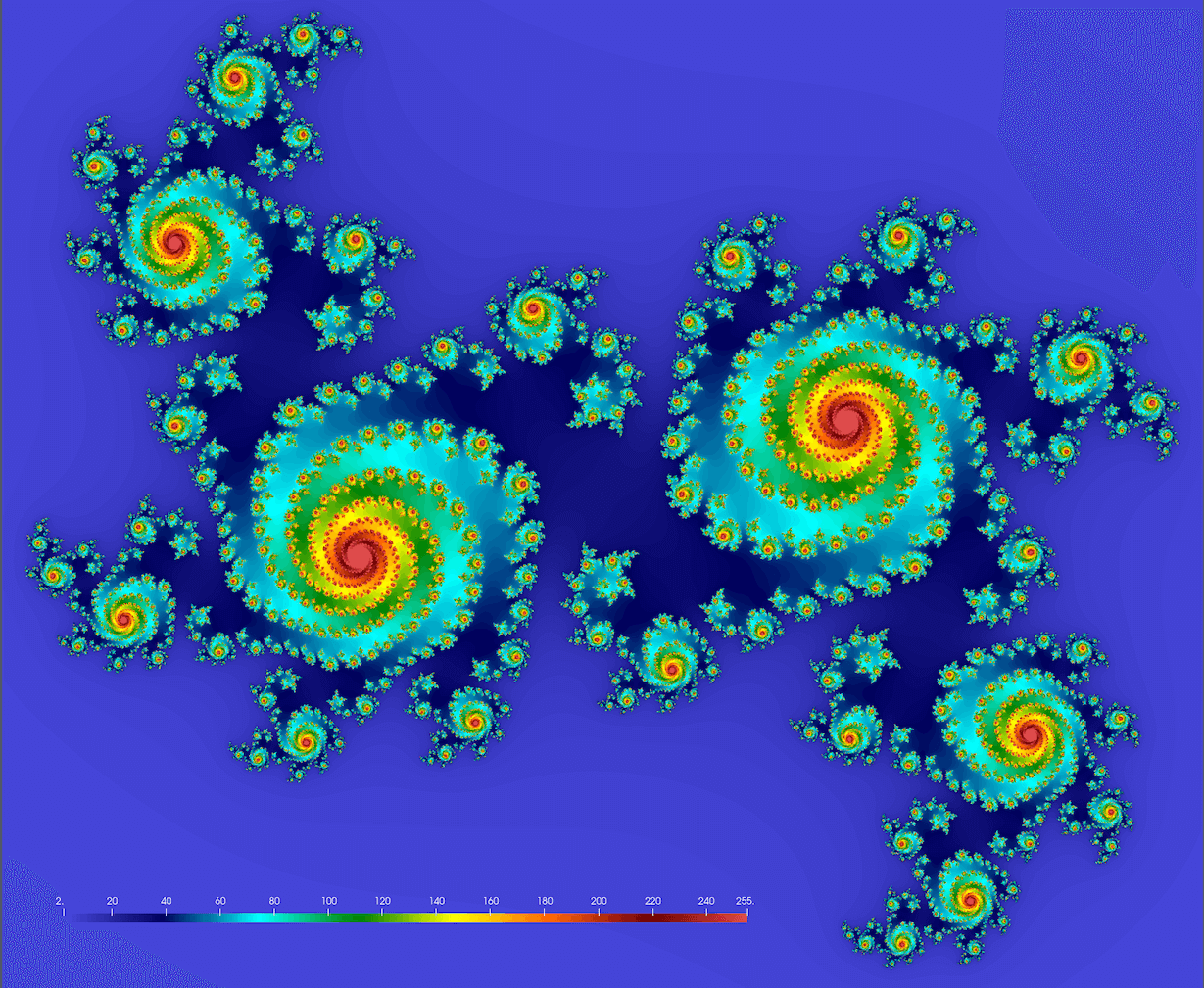
We should get something conceptually similar to this figure (here $c = 0.355 + 0.355i$; we’ll get drastically different fractals for different values of $c$):

Note: you might want to try these values too:

$c = 1.2e^{1.1πi}$ $~\Rightarrow~$ original textbook example
$c = -0.4-0.59i$ and 1.5X zoom-out $~\Rightarrow~$ denser spirals
$c = 1.34-0.45i$ and 1.8X zoom-out $~\Rightarrow~$ beans
$c = 0.34-0.05i$ and 1.2X zoom-out $~\Rightarrow~$ connected spiral boots

Below is the serial code juliaSetSerial.chpl:

use Time;

config const height, width = 2_000;   // 2000^2 image
var watch: stopwatch;
config const save = false;

proc pixel(z0) {
  const c = 0.355 + 0.355i;
  var z = z0*1.2;   // zoom out
  for i in 1..255 do {
    z = z*z + c;
    if z.re**2+z.im**2 >= 16 then // abs(z)>=4 does not work with LLVM
      return i;
  }
  return 255;
}

writeln("Computing ", height, "x", width, " Julia set ...");
watch.start();
var stability: [1..height,1..width] int;
for i in 1..height do {
  var y = 2*(i-0.5)/height - 1;
  for j in 1..width do {
    var point = 2*(j-0.5)/width - 1 + y*1i;
    stability[i,j] = pixel(point);
  }
}
watch.stop();
writeln('It took ', watch.elapsed(), ' seconds');

source ~/startMultiLocaleGPU.sh
module load netcdf/4.9.2
chpl  --fast juliaSetSerial.chpl
./juliaSetSerial -nl 1

It took me 2.34679 seconds to compute a $2000^2$ fractal.

Let’s port it to a GPU!

step 1 (optional)
> if here.gpus.size == 0 {
>   writeln("need a GPU ...");
>   exit(1);
> }

step 2
< proc pixel(z0) {
---
> proc pixel(x0,y0) {

step 3
<   var z = z0*1.2;   // zoom out
---
>   var x = x0*1.2;   // zoom out
>   var y = y0*1.2;   // zoom out

step4
<     z = z*z + c;
---
>     var xnew = x**2 - y**2 + c.re;
>     var ynew = 2*x*y + c.im;
>     x = xnew;
>     y = ynew;

step 5
<     if z.re**2+z.im**2 >= 16 then // abs(z)>=4 does not work with LLVM
---
>     if x**2+y**2 >= 16 then

step 6
< var stability: [1..height,1..width] int;
---
> on here.gpus[0] {
>   var stability: [1..height,1..width] int;
...
> }

step 7
< for i in 1..height do {
---
>   @assertOnGpu
>   foreach i in 1..height with (ref stability) do {

step 8
<     var point = 2*(j-0.5)/width - 1 + y*1i;
<     stability[i,j] = pixel(point);
---
>       var x = 2*(j-0.5)/width - 1;
>       stability[i,j] = pixel(x,y);

Here is the full GPU version:

use Time;

config const height, width = 2_000;   // 2000^2 image
var watch: stopwatch;
config const save = false;

if here.gpus.size == 0 {
  writeln("need a GPU ...");
  exit(1);
}

proc pixel(x0,y0) {
  const c = 0.355 + 0.355i;
  var x = x0*1.2; // zoom out
  var y = y0*1.2; // zoom out
  for i in 1..255 do {
    var xnew = x**2 - y**2 + c.re;
    var ynew = 2*x*y + c.im;
    x = xnew;
    y = ynew;
    if x**2+y**2 >= 16 then
      return i;
  }
  return 255;
}

writeln("Computing ", height, "x", width, " Julia set ...");
watch.start();
on here.gpus[0] {
  var stability: [1..height,1..width] int;
  @assertOnGpu
  foreach i in 1..height with (ref stability) do {
    var y = 2*(i-0.5)/height - 1;
    for j in 1..width do {
      var x = 2*(j-0.5)/width - 1;
      stability[i,j] = pixel(x,y);
    }
  }
}
watch.stop();
writeln('It took ', watch.elapsed(), ' seconds');

It took 0.017364 seconds on the GPU.

Problem size	CPU time in sec	GPU time in sec
$2000\times 2000$	1.64477	0.017372
$4000\times 4000$	6.5732	0.035302
$8000\times 8000$	26.1678	0.067307
$16000\times 16000$	104.212	0.131301

Reduction operations

Both the prime factorization problem and the Julia set problem compute elements of a large array in parallel on a GPU, but they don’t do any reduction (combining multiple numbers into one). It turns out, you can do reduction operations on a GPU with the usual reduce intent in a parallel loop:

config const n = 1e8: int;
var total = 0.0;
on here.gpus[0] {
  forall i in 1..n with (+ reduce total) do
    total += 1.0 / i**2;
  writef("total = %{###.###############}\n", total);
}

Alternatively, you can use built-in reduction operations on an array (that must reside in GPU-accessible memory), e.g.

use GPU;
config const n = 1e8: int;
on here.gpus[0] {
  var a: [1..n] real;
  forall i in 1..n do
    a[i] = 1.0 / i**2;
  writef("total = %{###.###############}\n", gpuSumReduce(a));
}

Other supported array reduction operations on GPUs are gpuMinReduce(), gpuMaxReduce(), gpuMinLocReduce() and gpuMaxLocReduce().

Running GPU Chapel on the Alliance systems

Running GPU Chapel on your computer

Useful built-in variables

Our first GPU code

Alternative syntax

Demo

GPU diagnostics

Verifying if a loop can run on a GPU

Timing on the CPU

Timing on the GPU

Prime factorization of each element of a large array

Finer control

Multiple locales and multiple GPUs

Demo

Demo

Use GPU features without a GPU and/or vendor SDK

Porting the Julia set problem to a GPU

Reduction operations

Links