Parallelizing the Julia set problem
This project is a mathematical problem to compute a Julia set,
defined as a set of points on the complex plane that remain bound under infinite recursive transformation
- pick a point
- compute iterations
- store the iteration number
- limit max iterations at 255
4.1 if
4.2 the quicker a point diverges, the lower its - plot
We should get something conceptually similar to this figure (here
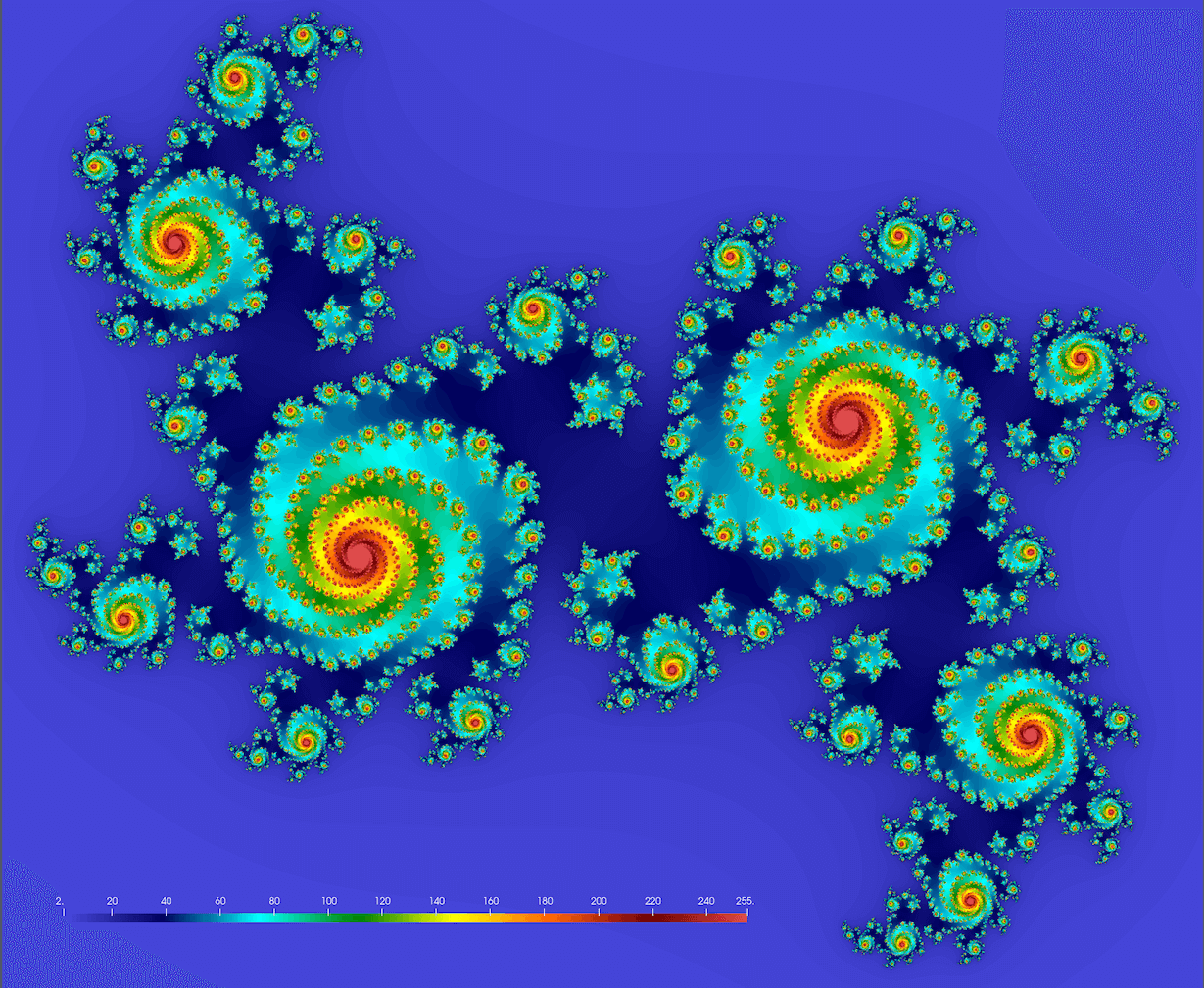
Note: you might want to try these values too:
Below is the serial code juliaSetSerial.chpl:
use Time;
use NetCDF.C_NetCDF;
proc pixel(z0) {
const c = 0.355 + 0.355i;
var z = z0*1.2; // zoom out
for i in 1..255 do {
z = z*z + c;
if abs(z) >= 4 then
return i:c_int;
}
return 255:c_int;
}
const height, width = 2_000; // 2000^2 image
var point: complex, y: real, watch: stopwatch;
writeln("Computing Julia set ...");
var stability: [1..height,1..width] c_int;
watch.start();
for i in 1..height do {
y = 2*(i-0.5)/height - 1;
for j in 1..width do {
point = 2*(j-0.5)/width - 1 + y*1i; // rescale to -1:1 in the complex plane
stability[i,j] = pixel(point);
}
}
watch.stop();
writeln('It took ', watch.elapsed(), ' seconds');
The reason we are using C types (c_int) here – and not Chapel’s own int(32) or int(64) – is that we can
save the resulting array stability into a compressed netCDF file. To the best of my knowledge, this can only
be done using NetCDF.C_NetCDF library that relies on C types. You can add this to your code:
writeln("Writing NetCDF ...");
use NetCDF.C_NetCDF;
proc cdfError(e) {
if e != NC_NOERR {
writeln("Error: ", nc_strerror(e): string);
exit(2);
}
}
var ncid, xDimID, yDimID, varID: c_int;
var dimIDs: [0..1] c_int; // two elements
cdfError(nc_create("test.nc", NC_NETCDF4, ncid)); // const NC_NETCDF4 => file in netCDF-4 standard
cdfError(nc_def_dim(ncid, "x", width, xDimID)); // define the dimensions
cdfError(nc_def_dim(ncid, "y", height, yDimID));
dimIDs = [xDimID, yDimID]; // set up dimension IDs array
cdfError(nc_def_var(ncid, "stability", NC_INT, 2, dimIDs[0], varID)); // define the 2D data variable
cdfError(nc_def_var_deflate(ncid, varID, NC_SHUFFLE, deflate=1, deflate_level=9)); // compress 0=no 9=max
cdfError(nc_enddef(ncid)); // done defining metadata
cdfError(nc_put_var_int(ncid, varID, stability[1,1])); // write data to file
cdfError(nc_close(ncid));
Testing on my laptop, it took the code 0.471 seconds to compute a
Try running it yourself! It will produce a file test.nc that you can download to your computer and render
with ParaView or other visualization tool. Does the size of test.nc make sense?
Now let’s parallelize this code with forall. Copy juliaSetSerial.chpl into juliaSetParallel.chpl and
start modifying it:
- For the outer loop, replace
forwithforall. This will produce an error about the scope of variablesyandpoint:
error: cannot assign to const variable
note: The shadow variable '...' is constant due to forall intents in this loop
Discussion
Why do you think this message was produced? How do we solve this problem?
- What do we do next?
Once you have the working shared-memory parallel code, study its performance.
Discussion
Why do you think the code’s speed does not scale linearly with the number of cores?