Multi-threading with Base.Threads



 Table of contents

Important: Today we are working on a compute node inside an interactive job scheduled with salloc. Do not run Julia on the login node!

Let’s start Julia by typing julia in bash:

using Base.Threads   # otherwise would have to preface all functions/macros with 'Threads.'
nthreads()           # by default, Julia starts with a single thread of execution

If instead we start with julia -t 2 (or prior to v1.5 with JULIA_NUM_THREADS=2 julia):

using Base.Threads
nthreads()           # now we have access to 2 threads

When launched from this interface, these two threads will run on two CPU cores on a compute node.

Let’s run our first multi-threaded code:

@threads for i=1:10   # parallel for loop using all threads
    println("iteration $i on thread $(threadid())")     # notice bash-like syntax
end

This would split the loop between 2 threads running on two CPU cores: each core would be running one thread.

Let’s now fill an array with values in parallel:

a = zeros(Int32, 10)    # 32-bit integer array
@threads for i=1:10
    a[i] = threadid()   # should be no collision: each thread writes to its own part
end
a

Here we are filling this array in parallel, and no thread will overwrite another thread’s result. In other words, this code is thread-safe.

Note: @threads macro is well-suited for shared-memory data parallelism without any reduction. Curiously, @threads does not have any data reduction built-in, which is a serious omission that will likely be addressed in future versions.

Let’s initialize a large floating array and fill it with values in serial and time the loop. We’ll package the code into a function to get more accurate timing with/without @threads.

n = Int64(1e8)     # integer number
n = 100_000_000    # another way of doing this

function test(n)   # serial code
    a = zeros(n);
    for i in 1:n
        a[i] = log10(i)
    end
end

@time test(n)

On the training cluster in three runs I get 2.52s, 2.45s, 2.43s.

The multi-threaded code performs faster:

using Base.Threads
nthreads()         # still running 2 threads

function test(n)   # multi-threaded code
    a = zeros(n);
    @threads for i in 1:n
        a[i] = log10(i)
    end
end

@time test(n)

– on the same cluster I see 1.49s, 1.54s, 1.41s. If I reschedule the job with --cpus-per-task=4 and use julia -t 4, the times change to 0.84s, 0.93s, 0.79s.

Note: There is also @btime from BenchmarkTools package that has several advantages over @time. We will switch to it soon.

Let’s add reduction

We will compute the sum $\sum_{i=1}^{10^6}i$ with multiple threads. Consider this code:

total = 0
@threads for i = 1:Int(1e6)
    global total += i          # use `total` from global scope
end
println("total = ", total)

This code is not thread-safe:

  • race condition: multiple threads updating the same variable at the same time
  • a new result every time
  • unfortunately, @threads does not have built-in reduction support

Let’s make it thread-safe (one of many possible solutions) using an atomic variable total. Only one thread can update an atomic variable at a time; all other threads have to wait for this variable to be released before they can write into it.

total = Atomic{Int64}(0)
@threads for i in 1:Int(1e6)
    atomic_add!(total, i)
end
println("total = ", total[])   # need to use [] to access atomic variable's value

Now every time we get the same result. This code is supposed to be much slower: threads are waiting for others to finish updating the variable, so with let’s say 4 threads and one variable there should be a lot of waiting … Atomic variables were not really designed for this type of usage … Let’s do some benchmarking!

Benchmarking in Julia

We already know that we can use @time macro for timing our code. Let’s do summation of integers from 1 to Int64(1e8) using a serial code:

n = Int64(1e8)
total = Int128(0)   # 128-bit for the result!
@time for i in 1:n
	global total += i
end
println("total = ", total)

On the training cluster I get 10.87s, 10.36s, 11.07s. Here @time also includes JIT compilation time (marginal here). Let’s switch to @btime from BenchmarkTools: it runs the code several times, reports the shortest time, and prints the result only once. Therefore, with @btime you don’t need to precompile the code.

using BenchmarkTools
n = Int64(1e8)
@btime begin
    total = Int128(0)   # 128-bit for the result!
	for i in 1:n
	    total += i
	end
end
println("total = ", total)

10.865 s

Next we’ll package this code into a function:

function quick(n)
    total = Int128(0)   # 128-bit for the result!
    for i in 1:n
        total += i
    end
    return(total)
end

@btime quick(Int64(1e8))    # correct result, 1.826 ns runtime
@btime quick(Int64(1e9))    # correct result, 1.825 ns runtime
@btime quick(Int64(1e15))   # correct result, 1.827 ns runtime

In all these cases we see ~2 ns running time – this can’t be correct! What is going on here? It turns out that Julia is replacing the summation with the exact formula $$\frac{n(n+1)}{2}.$$

We want to:

  1. force computation $~\Rightarrow~$ we’ll compute something more complex than simple integer summation, so that it cannot be replaced with a formula
  2. exclude compilation time $~\Rightarrow~$ we’ll package the code into a function + precompile it
  3. make use of optimizations for type stability $~\Rightarrow~$ package into a function + precompile it
  4. time only the CPU-intensive loops

Slow series

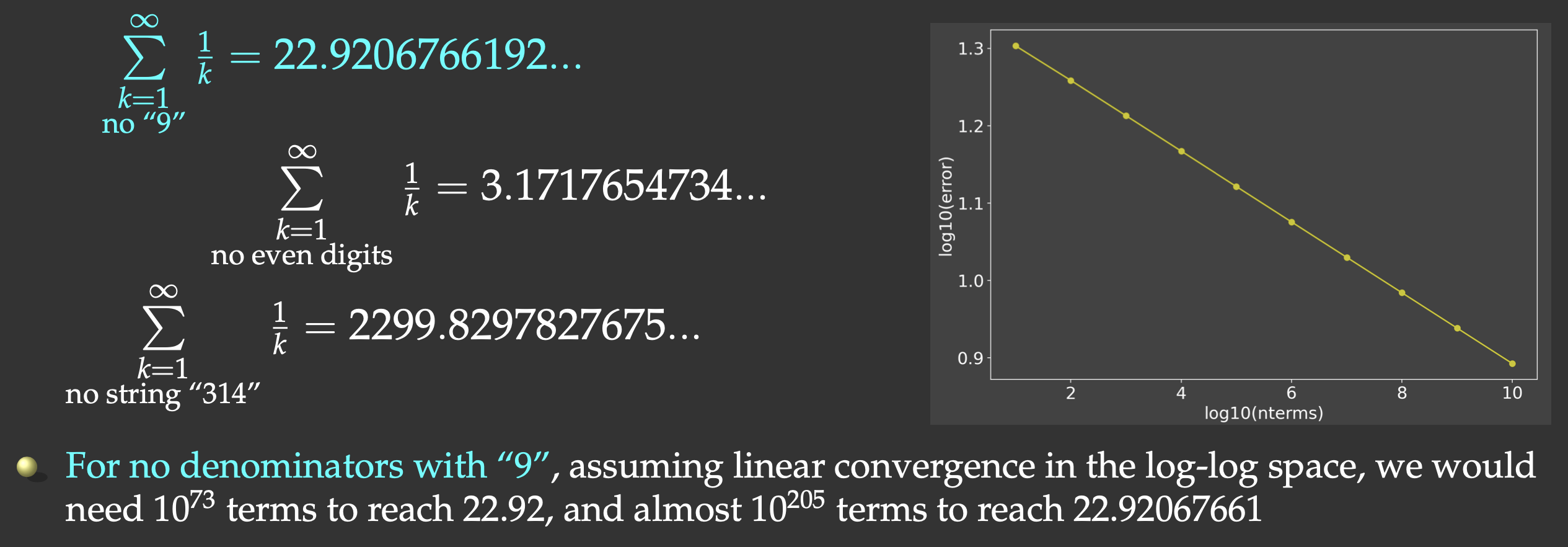
We could replace integer summation $\sum_{i=1}^\infty i$ with the harmonic series, however, the traditional harmonic series $\sum\limits_{k=1}^\infty{1\over k}$ diverges. It turns out that if we omit the terms whose denominators in decimal notation contain any digit or string of digits, it converges, albeit very slowly (Schmelzer & Baillie 2008), e.g.

But this slow convergence is actually good for us: our answer will be bounded by the exact result (22.9206766192…) on the upper side. We will sum all the terms whose denominators do not contain the digit “9”.

We will have to check if “9” appears in each term’s index i. One way to do this would be checking for a substring in a string:

if !occursin("9", string(i))
    <add the term>
end

It turns out that integer exclusion is ∼4X faster (thanks to Paul Schrimpf from the Vancouver School of Economics @UBC for this code!):

function digitsin(digitSequence::Int, num)   # decimal representation of `digitSequence` has N digits
    base = 10
    while (digitSequence ÷ base > 0)   # `digitSequence ÷ base` is same as `floor(Int, digitSequence/base)`
        base *= 10
    end
    # `base` is now the first Int power of 10 above `digitSequence`, used to pick last N digits from `num`
    while num > 0
        if (num % base) == digitSequence     # last N digits in `num` == digitSequence
            return true
        end
        num ÷= 10                     # remove the last digit from `num`
    end
    return false
end
if !digitsin(9, i)
    <add the term>
end

Let’s now do the timing of our serial summation code with 1e8 terms:

function slow(n::Int64, digitSequence::Int)
    total = Float64(0)    # this time 64-bit is sufficient!
    for i in 1:n
        if !digitsin(digitSequence, i)
            total += 1.0 / i
        end
	end
    return total
end
@btime slow(Int64(1e8), 9)   # total = 13.277605949858103, runtime 2.986 s

1st multi-threaded version: using an atomic variable

Recall that with an atomic variable only one thread can write to this variable at a time: other threads have to wait before this variable is released, before they can write. With several threads running in parallel, there will be a lot of waiting involved, and the code should be relatively slow.

using Base.Threads
using BenchmarkTools
function slow(n::Int64, digitSequence::Int)
	total = Atomic{Float64}(0)
    @threads for i in 1:n
        if !digitsin(digitSequence, i)
            atomic_add!(total, 1.0 / i)
		end
    end
    return total[]
end
@btime slow(Int64(1e8), 9)

Exercise “Threads.1”

Put this version of slow() along with digitsin() into the file atomicThreads.jl and run it from the bash terminal (or from from REPL). First, time this code with 1e8 terms using one thread (serial run julia atomicThreads.jl). Next, time it with 2 or 4 threads (parallel run julia -t 2 atomicThreads.jl). Did you get any speedup? Make sure you obtain the correct numerical result.

With one thread I measured 2.838 s. The runtime stayed essentially the same (now we are using atomic_add()) which makes sense: with one thread there is no waiting for the variable to be released.

  • With 2 threads, I measured XXX – let’s discuss! Is this what we expected?
  • With 4 threads, I measured YYY – let’s discuss! Is this what we expected?

Exercise “Threads.2”

Let’s run the previous exercise as a batch job with sbatch. Hint: you will need to go to the login node and submit a multi-core job with sbatch shared.sh. When finished, do not forget to go back to (or restart) your interactive job.

2nd version: alternative thread-safe implementation

In this version each thread is updating its own sum, so there is no waiting for the atomic variable to be released? Is this code faster?

using Base.Threads
using BenchmarkTools
function slow(n::Int64, digitSequence::Int)
    total = zeros(Float64, nthreads())
    @threads for i in 1:n
        if !digitsin(digitSequence, i)
            total[threadid()] += 1.0 / i
        end
    end
    return sum(total)
end
@btime slow(Int64(1e8), 9)

Update: Pierre Fortin brought to our attention the false sharing effect. It arises when several threads are writing into variables placed close enough to each other to end up in the same cache line. Cache lines (typically ~32-128 bytes in size) are chunks of memory handled by the cache. If any two threads are updating variables (such as two neighbouring elements in our total array here) that end up in the same cache line, the cache line will have to migrate between the two threads’ caches, reducing the performance.

In general, you want to align shared global data (thread partitions in the array total in our case) to cache line boundaries, or avoid storing thread-specific data in an array indexed by the thread id or rank. Pierre suggested a solution using the function space() which introduces some spacing between array elements so that data from different threads do not end up in the same cache line:

using Base.Threads
using BenchmarkTools

function digitsin(digitSequence::Int, num)   # decimal representation of `digitSequence` has N digits
    base = 10
    while (digitSequence ÷ base > 0)   # `digitSequence ÷ base` is same as `floor(Int, digitSequence/base)`
        base *= 10
    end
    # `base` is now the first Int power of 10 above `digitSequence`, used to pick last N digits from `num`
    while num > 0
        if (num % base) == digitSequence     # last N digits in `num` == digitSequence
            return true
        end
        num ÷= 10                     # remove the last digit from `num`
    end
    return false
end

 # Our initial function:
function slow(n::Int64, digitSequence::Int)
    total = zeros(Float64, nthreads())
    @threads for i in 1:n
        if !digitsin(digitSequence, i)
            total[threadid()] += 1.0 / i
        end
    end
    return sum(total)
end

 # Function optimized to prevent false sharing:
function space(n::Int64, digitSequence::Int)
    space = 8 # assume a 64-byte cache line, hence 8 Float64 elements per cache line
    total = zeros(Float64, nthreads()*space)
    @threads for i in 1:n
        if !digitsin(digitSequence, i)
            total[threadid()*space] += 1.0 / i
        end
    end
    return sum(total)
end

@btime slow(Int64(1e8), 9)
@btime space(Int64(1e8), 9)

Here are the timings from two successive calls to slow() and space() on the the training cluster:

[~/tmp]$ julia separateSums.jl 
  2.836 s (7 allocations: 656 bytes)
  2.882 s (7 allocations: 704 bytes)
[~/tmp]$ julia -t 4 separateSums.jl 
  935.609 ms (23 allocations: 2.02 KiB)
  687.972 ms (23 allocations: 2.23 KiB)
[~/tmp]$ julia -t 10 separateSums.jl
  608.226 ms (53 allocations: 4.73 KiB)
  275.662 ms (54 allocations: 5.33 KiB)

The speedup is substantial!

We see similar speedup with space = 4, but not quite with space = 2, suggesting that we are dealing with 32-byte cache lines on our system.

3rd multi-threaded version: using heavy loops

This version is classical task parallelism: we divide the sum into pieces, each to be processed by an individual thread. For each thread we explicitly compute the start and finish indices it processes.

using Base.Threads
using BenchmarkTools
function slow(n::Int64, digitSequence::Int)
    numthreads = nthreads()
    threadSize = floor(Int64, n/numthreads)   # number of terms per thread (except last thread)
    total = zeros(Float64, numthreads);
    @threads for threadid in 1:numthreads
        local start = (threadid-1)*threadSize + 1
        local finish = threadid < numthreads ? (threadid-1)*threadSize+threadSize : n
        println("thread $threadid: from $start to $finish");
        for i in start:finish
            if !digitsin(digitSequence, i)
                total[threadid] += 1.0 / i
            end
        end
    end
    return sum(total)
end
@btime slow(Int64(1e8), 9)

Let’s time this version together with heavyThreads.jl: 984.076 ms – is this the fastest version?

Exercise “Threads.3”

Would the runtime be different if we use 2 threads instead of 4?

Finally, below are the timings on Cedar with heavyThreads.jl. Note that the times reported here were measured with 1.6.2. Going from 1.5 to 1.6, Julia saw quite a big improvement (~30%) in performance, plus a CPU on Cedar is different from a vCPU on the training cluster, so treat these numbers only as relative to each other.

#!/bin/bash
#SBATCH --ntasks=1
#SBATCH --cpus-per-task=...
#SBATCH --mem-per-cpu=3600M
#SBATCH --time=00:10:00
#SBATCH --account=def-someuser
module load julia
julia -t $SLURM_CPUS_PER_TASK heavyThreads.jl
Code serial 2 cores 4 cores 8 cores 16 cores
Time 7.910 s 4.269 s 2.443 s 1.845 s 1.097 s

Task parallelism with Base.Threads: building a dynamic scheduler

In addition to @threads (automatically parallelize a loop with multiple threads), Base.Threads includes Threads.@spawn that runs a task (an expression / function) on any available thread and then immediately returns to the main thread.

Consider this:

using Base.Threads
import Base.Threads: @spawn # has to be explicitly imported to avoid potential conflict with Distributed.@spawn
nthreads()                  # make sure you have access to multiple threads
threadid()                  # always shows 1 = local thread
fetch(@spawn threadid())    # run this function on another available thread and get the result

Every time you run this, you will get a semi-random reponse, e.g.

for i in 1:30
    print(fetch(@spawn threadid()), " ")
end

You can think of @spawn as a tool to dynamically offload part of your computation to another thread – this is classical task parallelism, unlike @threads which is data parallelism.

With @spawn it is up to you to write an algorithm to subdivide your computation into multiple threads. With a large loop, one possibility is to divide the loop into two pieces, offload the first piece to another thread and run the other one locally, and then recursively subdivide these pieces into smaller chunks. With N subdivisions you will have 2^N tasks running on a fixed number of threads, and only one of these tasks will not be scheduled with @spawn.

using Base.Threads
import Base.Threads: @spawn
using BenchmarkTools

function digitsin(digitSequence::Int, num)
    base = 10
    while (digitSequence ÷ base > 0)
        base *= 10
    end
    while num > 0
        if (num % base) == digitSequence
            return true
        end
        num ÷= 10
    end
    return false
end

@doc """
a, b are the left and right edges of the current interval;
numsubs is the number of subintervals, each will be assigned to a thread;
numsubs will be rounded up to the next power of 2,
i.e. setting numsubs=5 will effectively use numsubs=8
""" ->
function slow(n::Int64, digitSequence::Int, a::Int64, b::Int64, numsubs=16)
    if b-a > n/numsubs    # (n/numsubs) is our iteration target per thread
        mid = (a+b)>>>1   # shift by 1 bit to the right
        finish = @spawn slow(n, digitSequence, a, mid, numsubs)
        t2 = slow(n, digitSequence, mid+1, b, numsubs)
        return fetch(finish) + t2
    end
    t = Float64(0)
	println("computing on thread ", threadid())
    for i in a:b
        if !digitsin(digitSequence, i)
            t += 1.0 / i
        end
    end
    return t
end

n = Int64(1e8)
@btime slow(n, 9, 1, n, 1)   # run the code in serial (one interval, use one thread)
@btime slow(n, 9, 1, n, 4)   # 4 intervals, all but one spawned on one of `nthreads()` threads

There are two important considerations here:

  1. Depending on the number of subintervals, Julia might decide not to use all four threads! To ensure best load balancing, consider using a very large number of subintervals, to fully saturate all cores, e.g. numsubs=128 with 4 threads.
  2. The println line might significantly slow down the code (depending on your processor architecture), as all threads write into an output buffer and – with many threads – take turns doing this, with some waiting involved. You might want to comment out println to get the best performance.

With these two points in mind, try to get 100% parallel efficiency.